Functions and Their Inverses

Composition of Functions

Consider the functions $f$ and $g$, such that $f$ is evaluated at $g(x)$ . This creates a new function $f \circ g$ which is a composite function of $f$ and $g$ and defined as follows: $$(f \circ g)(x) = f\left( g(x) \right) $$

This is illustrated by the following diagram:



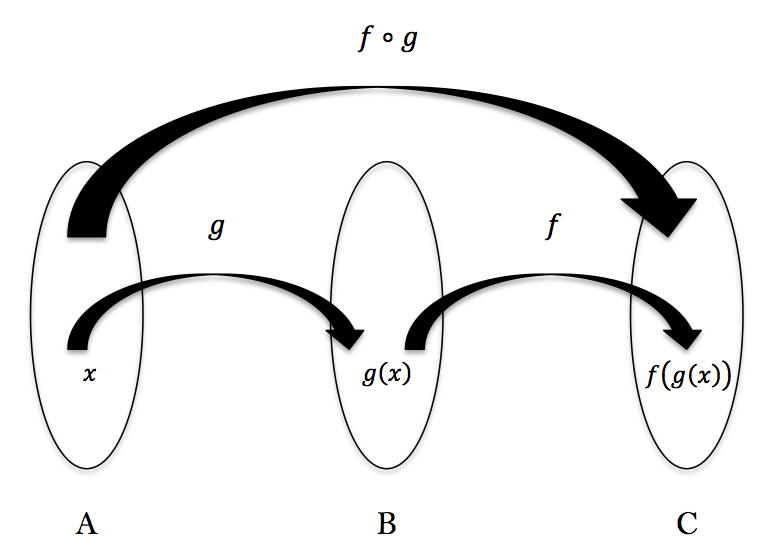
Although new vocabulary has been introduced, you have already been exposedto the concept of composing functions. Recall exercise 2(a) in the previous lesson. You were given the function $h(x) = \frac{2\sqrt{x+4}}{|1-x|},$ and asked to evaluate $h(x^2+4x)$. Here, $h(x)$ was being composed with the quadratic function $g(x) = x^2+4x$!



To determine the range of a composition of functions, you take the range of the outermost function and determine if the domain (which is now the range of the inner function) is going to eliminate any of those points. For example:

Example.

Find the domain and range of $ k(h(x)) = \sqrt{\frac{1}{x-2}},$ where $k(x)=\sqrt{x}$ and $h(x)=\frac{1}{x-2}.$

Solution. First notice that $domain\left( h(x) \right) = \{ x\in \mathbb{R}\; \large| \; x \neq 2\}.$ Furthermore, $$ domain\left( k(h(x)) \right) = \{ x\in \mathbb{R}\; \large| \; \frac{1}{x-2} \geq 0 \} = \{ x \in \mathbb{R} \; \large| \; x > 2 \} .$$ Therefore: \begin{align*} domain\left( ( k \circ h)(x)\right) &= domain \left( h(x) \right) \cap domain \left( k(h(x)) \right) \\ &= domain\left(\frac{1}{x-2}\right) \cap domain\left(\sqrt{\frac{1}{x-2}}\right) \\ &=\{ x\in \mathbb{R}\; \large| \; x \neq 2\} \cap \{ x \in \mathbb{R} \; \large| \; x > 2 \} \\ &= \{ x \in \mathbb{R} \; \large| \; x > 2 \}. \end{align*} For the range, we first consider the range of $k(x).$ Since $k(x)=\sqrt{x},$ we know that the range is $\{ y \in \mathbb{R} \; \large| \; y \geq 0 \}$. Now, because the range of $h(x)$ includes every positive $y$− value except zero, we know that $k(h(x))\neq k(0)=0.$ Furthermore, since no other $x$− value makes $k(x)=0,$ the number zero is not in the range of $k(h(x))$ . The range is therefore the set $\{ y \in \mathbb{R} \; \large| \; y > 0 \}.$

Example.

Move the point $a$ or change the functions $f(x)$ and $g(x)$ to see how it affects the composition $g\big(f(x)\big)$.

Exercises

1.	Find two functions $f$ and $g$ such that $f \circ g$ yields the following function (note: there are many possible solutions):
	a) $F(x)=\sqrt[5]{\sqrt{x}-1}$
	Solution: Let $ f(x) = \sqrt[5]{x}$ and $g(x)=\sqrt{x}-1$
	b) $G(x) = \frac{4}{x^2+7}$
	Solution. Let $f(x) = \frac{4}{x+7}$ and $g(x)=x^2$
	c) $H(x) = |8-x^7|$
	Solution. Let $f(x) = |x|$ and $g(x)=8-x^7$
2.	Consider $f(x)=\frac{3}{x}$ and $g(x)=\sqrt{5-x}.$ Find the following functions: a) $f \circ g, \qquad $ b) $g \circ f, \qquad $ c) $g \circ g, \qquad $ d) $f \circ f$
	a) $f \circ g$
	Solution: \begin{align*}(f\circ g)(x) &= f(g(x)) \\ &= \frac{3}{\sqrt{5-x}} \end{align*}
	b) $g \circ f$
	Solution. \begin{align*} (g \circ f)(x) &= g(f(x)) \\ &=\sqrt{5-\left( \frac{3}{x} \right)} \\ &= \sqrt{\frac{5x-3}{x}} \end{align*}
	c) $g \circ g$
	Solution. \begin{align*} (g \circ g)(x) &= g(g(x)) \\ &=\sqrt{5-\sqrt{5-x}} \end{align*}
	d) $f \circ f$
	Solution. \begin{align*} (f \circ f)(x) &= f(f(x)) \\ &= \frac{3}{\left( \frac{3}{x} \right)} \\ &= \frac{3}{1}\cdot \frac{x}{3} \\ &= x \end{align*}
3.	Find the domains of the functions found in parts 2(a - d):
	a)
	Solution: \begin{align*} domain\left( ( f \circ g)(x)\right) &= domain \left( g(x) \right) \cap domain \left( f(g(x)) \right) \\ &= domain\left(\sqrt{5-x} \right) \cap domain\left( \frac{3}{\sqrt{5-x}} \right) \\ &=\{ x \in \mathbb{R}\; \large| \; x \leq 5 \} \cap \{ x \in \mathbb{R} \; \large| \; x-5 > 0 \} \\ &=\{ x \in \mathbb{R}\; \large| \; x \leq 5 \} \cap \{ x \in \mathbb{R} \; \large| \; x < 5\} \\ &= \{ x \in \mathbb{R} \; \large| \; x < 5\} \end{align*}
	b)
	\begin{align*} domain\left( ( g \circ f)(x)\right) &= domain \left( f(x) \right) \cap domain \left( g(f(x)) \right) \\ &= domain\left(\frac{3}{x} \right) \cap domain\left( \sqrt{\frac{5x-3}{x}} \right) \\ &=\{ x \in \mathbb{R}\; \large| \; x \neq 0 \} \cap \left\{ x \in \mathbb{R} \; \large| \; \frac{5x-3}{x} \geq 0 \right\} \end{align*} Now we must solve the following inequality: $\frac{5x-3}{x}\geq 0$. We will omit the details of this, but refer to the previous lesson Intervals in the Inequalities and Absolute Value topic to see how to solve similar inequalities. Using these techniques, we find that this inequality holds for $x$ in $(-\infty,0)\cup [\frac{3}{5}, \infty)$, i.e. $$domain(g(f(x)) = \left\{ x \in \mathbb{R}\; \large| \; x < 0 \textrm{ or } x \geq \frac{3}{5} \right\}.$$ Therefore, \begin{align*} domain\left( ( g \circ f)(x)\right) &= domain \left( f(x) \right) \cap domain \left( g(f(x)) \right) \\ &=\{ x \in \mathbb{R}\; \large| \; x \neq 0 \} \cap \left\{ x \in \mathbb{R} \; \large| \; x < 0 \textrm{ or } x \geq \frac{3}{5}\right\} \\ &= \left\{ x \in \mathbb{R} \; \large| \; x < 0 \textrm{ or } x \geq \frac{3}{5}\right\} \end{align*}
	c) $domain(g\circ g)$
	Solution. First notice that $domain(g\circ g)(x) = \sqrt{5-\sqrt{5-x}}$ requires $5-\sqrt{5-x} \geq 0.$ So we'll begin by solving the inequality. Restriction 1: $x \leq 5,$ since $\sqrt{5-x}$ must be defined. Restriction 2: \begin{align*}$5-\sqrt{5-x} \geq 0 &\Rightarrow \sqrt{5-x} \leq 5 \\ \textrm{squaring both sides} &\Rightarrow 5-x \leq 25 \\ &\Rightarrow -x \leq 20 \\ &\Rightarrow x \geq -20. \end{align*} Combining Restrictions 1 and 2, we have: $-20 \leq x \leq 5$. Therefore \begin{align*} domain\left( ( g \circ g)(x)\right) &= domain \left( g(x) \right) \cap domain \left( g(g(x)) \right) \\ &= domain \left( \sqrt{5-x} \right) \cap domain \left( \sqrt{5-\sqrt{5-x}} \right) \\ &=\{ x \in \mathbb{R}\; \large| \; x \leq 5 \} \cap \{ x \in \mathbb{R} \; \large| \; 5-\sqrt{5-x} \geq 0 \} \\ &=\{ x \in \mathbb{R}\; \large| \; x \leq 5 \} \cap \{ x \in \mathbb{R} \; \large| \; -20 \leq x \leq 5 \} \\ &= \{ x \in \mathbb{R} \; \large| \; -20 \leq x \leq 5 \} \end{align*}
	d) $domain(f\circ f)$
	Solution. \begin{align*} domain\left( ( f \circ f)(x)\right) &= domain \left( f(x) \right) \cap domain \left( f(f(x)) \right) \\ &= domain \left( \frac{3}{x} \right) \cap domain \left( x \right) \\ &=\{ x \in \mathbb{R}\; \large| \; x \neq 0 \} \cap \{ x \in \mathbb{R} \} \\ &=\{ x \in \mathbb{R}\; \large| \; x \neq 0 \} \end{align*}
4.	Given the functions $f(x)=x^2-6$ and $g(x)=\sqrt{2x+5},$ evaluate and simplify the following: a) $(f \circ g)(2)- (g \circ f)(2), \qquad$ b) $(g \circ f \circ g)(0)$
	a) Solution: We can either first find the functions $f \circ g$ and $g\circ f$ and then perform the required evaluations, or we can immediately begin to evaluate, by starting from the inside. Let's proceed with the second option: \begin{align*} (f\circ g)(2) &= f(g(2)) \\ &= f\left( \sqrt{2(2)+5} \right) \\ &= f(\sqrt{9}) \\ &= f(3) \\ &= (3)^2 - 6\\ &= 9 - 6 \\ &= 3 \end{align*} \begin{align*} (g \circ f)(2) &= g(f(2)) \\ &= g( (2)^2-6)\\ &= g(-2) \\ &= f(3) \\ &= \sqrt{2(-2)+5} \\ &= \sqrt{1} \\ &= 1 \end{align*} Therefore, \begin{align*} (f \circ g)(2) - (g \circ f)(2) &=f(g(2)) - g(f(2)) \\ &= 3-1\\ &= 2 \end{align*}
	b) $(g \circ f \circ g)(0)$
	Solution. Using the same approach as part (a): \begin{align*} (g \circ f \circ g)(0) &= g \left( f(\sqrt{2(0)+5})\right) \\ &= g \left( f(\sqrt{5}) \right) \\ &= g \left( (\sqrt{5})^2 - 6 \right) \\ &= g(-1) \\ &= \sqrt{2(-1)+5} \\ &= \sqrt{3} \end{align*}