Inequalities

Intervals

We often use interval notation to express the solution set of an inequality. Here is a brief recap on the various type of intervals:

$(a,b) = \{ x \in \mathbb{R} | a < x < b \}$
$[a,b) = \{ x \in \mathbb{R} | a \leq x < b \}$
$(a,b] = \{ x \in \mathbb{R} | a < x \leq b \}$
$[a,b] = \{ x \in \mathbb{R} | a \leq x \leq b \}$
$(-\infty ,b) = \{ x \in \mathbb{R} | x < b \}$
$(-\infty ,b] = \{ x \in \mathbb{R} | x \leq b \}$
$(a,\infty) = \{ x \in \mathbb{R} | x>a \}$
$[a,\infty) = \{ x \in \mathbb{R} | x\geq a \}$
$(-\infty, \infty) = \mathbb{R}$

Example.

Solve $1\leq 2x+3 < 5$, sketch the solution set on the number line, and write it in terms of intervals.

$1 \leq 2x+3 < 5 $
$-2 \leq 2x < 2$	(Details)subtract 3 from both sides
$-1 \leq x < 1 $	(Details)divide both sides by 2

So the solution set is $[ -1 , 1)$.

In general, if you want to solve an inequality of the form $(x-a)(x-b) >0$ ($>$ can be replaced by $\geq, <, \leq$), notice that the factors $(x-a), (x-b)$ split the number line into 3 parts: $x< a$, $a < x < b$, $x > b$.

We can solve the inequality $(x-a)(x-b) >0$ by determining the sign of each factor on the three pieces.


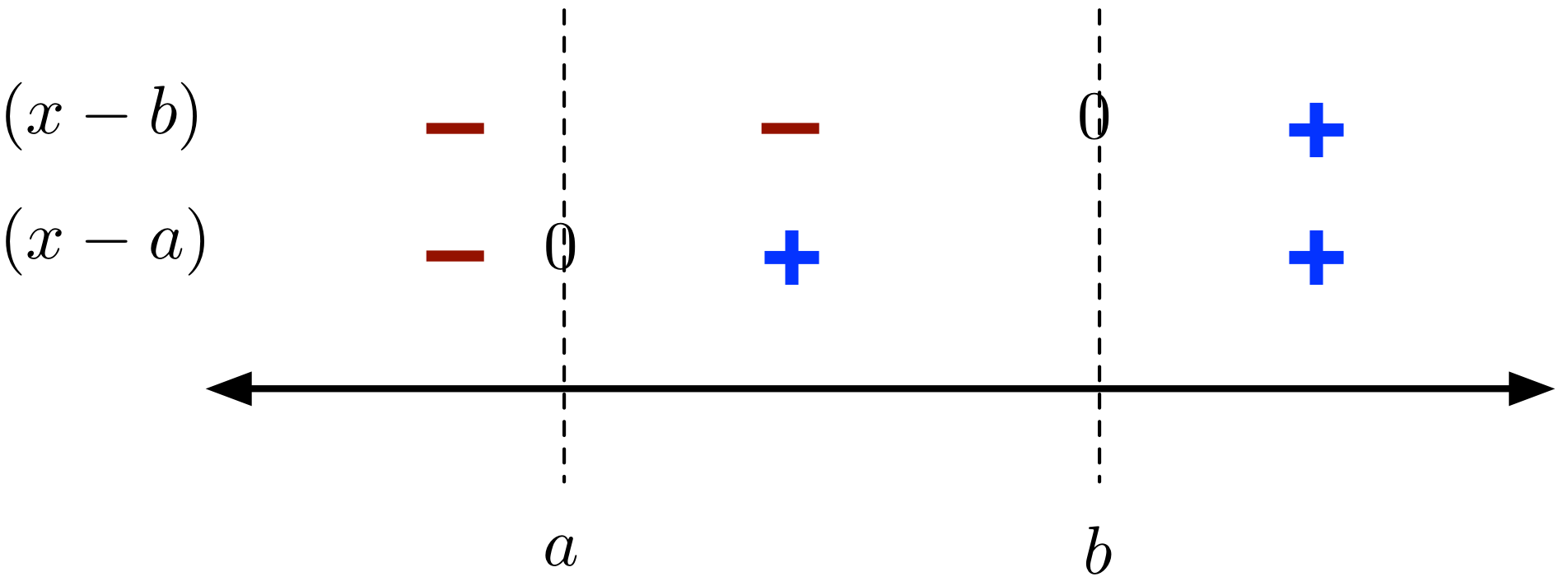
We can take a similar approach for inequalities with more than two factors. In this case, the line gets split into more pieces, however the approach is the same. You should determine the sign of the factors on each piece, and use them to solve the inequality. This technique suggests that when solving polynomial inequalities, it is often a good idea to rewrite the inequality by moving all non-zero terms to one side, then factoring, or completing the square (when factors cannot be found).

Example. Solve $x^{2} - x + 1 \geq 2x-1$, sketch the solution set on the number line, and write it in terms of intervals.

To solve this we begin by rewriting the inequality:

	$ x^{2} - x + 1 \geq 2x-1 $
$\Longleftrightarrow$	$x^{2} -3x +2 \geq 0$	(Details)move non-zero terms to one side
$\Longleftrightarrow$	$ (x-1)(x-2) \geq 0 $	(Details)factor the resulting polynomial

We are now left with the simpler inequality $(x-1)(x-2) \geq 0$, which we solve as follows:


This gives the solution $(-\infty, 1] \cup [2, \infty)$. (Details)The product of two terms is positive if either both terms are positive, or both terms are negative. And the product is $0$ if either term is $0$.


When dealing with inequalities that involve rational functions, you should move all non-zero terms to one side, then find a common denominator to obtain a simple inequality of the form $\frac{P(x)}{Q(x)} < 0$ (or $\leq , >, \geq$ as the case may be). We then take a similar approach to the one we did for a polynomial inequality. We try to factor the numerator and denominator, and use the factors to split the number line into pieces, and check the sign of the factors on each of the pieces. (Be mindful of where the denominator is equal to 0!)

Example. Solve the inequality $ x-3 \geq -\frac{4}{x} + 2$, sketch the solution set on the number line, and express it in interval form.

$ x-3 \geq -\frac{4}{x} + 2 $
$x-3 + \frac{4}{x} - 2 \geq 0 $	(Details)move all non-zero terms to one side
$ \frac{x(x-3)}{x} + \frac{4}{x} - \frac{2x}{x} \geq 0 $	(Details)find a common denominator
$ \frac{x^{2} - 5x + 4}{x} \geq 0 $	(Details)expand and simplify the top
$ \frac{(x-4)(x-1)}{x} \geq 0 $	(Details)factor top and bottom

This gives the solution $(0, 1] \cup [4, \infty)$. (Details)The product/quotient of three terms is positive if exactly two terms are negative, or all terms are positive. And the product/quotient is $0$ if either term in the numerator is $0$. However, we must be sure not to include values in our solution which would result in a $0$ in the denominator, like in this case, $0$.