Inequalities

Absolute Value

For any real number $a$, $|a|$ is the distance from $a$ to $0$ on the number line.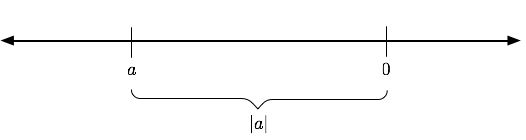


This means that the distance between $a$ and $b$ on the number line is given by $|b-a|$.

Alternatively, we can define $|a|$ as follows: If $a \geq 0$, then $|a| = a$, and if $a <0$, then $|a| = -a$.

We can also define $|a|$ by $|a| = \sqrt{a^{2}}$ where we take the positive square root.

Notice that for any $a \in \mathbb{R}$, $|a| \geq 0$, and $|a| = 0$ if and only if $a=0$.

All of the definitions are equivalent, and useful for various problems. For solving inequalities, the first definition is particularly useful.

Consider an inequality of the form $|x| < r$. From the first definition, we see that the solution set is the set of points whose distance from $0$ is less than $r$. In other words, the solution set is the interval $(-r, r)$.
To see this algebraically, note that $|x| < r$ is equivalent to the double inequality $-r < x < r$, which is exactly the interval $(-r, r)$.


The solution set of an inequality of the form $|x|>r$, is the set of points whose distance from $0$ is larger than $r$. In other words, the solution set is $(-\infty , -r) \cup (r, \infty)$.


Now consider an inequality of the form $|x-a| < r$. The solution set is the set of points whose distance from $a$ is less than $r$.
Algebraically, we get $-r < x-a < r \; $ or $\; a-r < x < a+r$, which is exactly the interval $(a-r, a+r)$.

Mini-Lecture.

Below is a mini lecture about absolute values.

Example. Solve the inequality $4 < | 2x+10| \leq 6$, sketch the solution set on the number line, and express it in interval form.

To deal with an inequality of this form, we should split it into two separate inequalities $4 < | 2x+10|$ and $| 2x+10| \leq 6$, then take the common solutions.
First we deal with the inequality $4 < | 2x+10|$:

$ 4 < | 2x+10| $
$ 2 < |x+5| $	(Details) divide both sides by 2
$ 2 < |x - (-5)| $	(Details)re-write it so that we can identify the solution set

From the last line we see that this gives the set of points whose distance is larger than 2 from $-5$. In interval notation this gives $( -\infty , -7) \cup (-3, \infty)$.

Now we deal with the inequality $| 2x+10| \leq 6$:

$ | 2x+10| \leq 6 $
$ |x+5| \leq 3 $	(Details) divide both sides by 2
$ |x - (-5)| \leq 3 $	(Details)re-write it so that we can identify the solution set

From the last line we see that this gives the set of points whose distance is less than or equal to 3 from $-5$. In interval notation this gives $[ -8, -2]$.

Now let's put this together. If we sketch the solutions to the inequalities we get:

From this we see that the common solutions are exactly $[-8, -7) \cup (-3, -2]$.