Graphing
Worked Examples
Some Transformations
We can sometimes obtain the graph of a function $y=f(x)$ from the graph of a simpler one by applying some of the following transformations:Part 1: Vertical stretch or compression
One type of transformation involves multiplying the whole function by a nonzero number. $$f(x) \longrightarrow af(x)$$ Let $g(x)=af(x)$. If $a<0$, the graph of $f(x)$ will be reflected about the $x$-axis to obtain the graph of $g(x)$. Furthermore:If $|a|<1$ the graph of $f(x)$ will be compressed vertically to obtain $g(x)$.
If $|a|>1$ the graph of $f(x)$ will be stretched vertically to obtain $g(x)$.
Example. Draw the graph of $y=-2\sin(x)$.
Solution: We can obtain it by, starting from the graph of $y=\sin(x)$, we first reflect through the $x$-axis and then stretch the graph by a factor of two. The result is: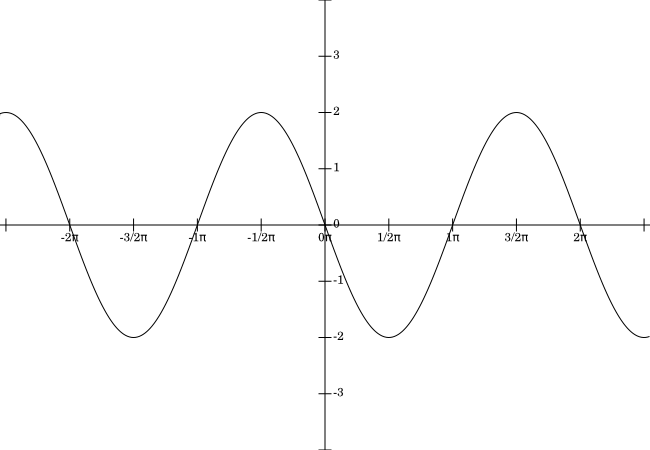
The graph of $y=-2\sin(x)$.
Part 2: Horizontal stretch or compression
We can also transform a function by multiplying the variable by a nonzero number. $$f(x) \longrightarrow f(bx)$$ Let $g(x)=f(bx)$. If $b<0$, the graph of $f(x)$ will be reflected through the $y$-axis to obtain the graph of $g(x)$. Furthermore:If $|b|<1$ the graph of $f(x)$ will be stretched horizontally to obtain $g(x)$.
If $|b|>1$ the graph of $f(x)$ will be compressed horizontally to obtain $g(x)$.
Example. Draw the graph of $y=\tan\left(\frac{x}{3}\right)$.
Solution: We can start from the graph of $y=\tan(x)$ and stretch it by a factor of $3$.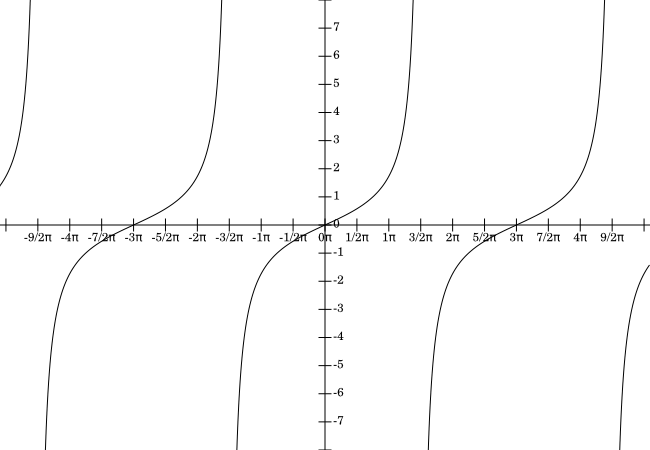
The graph of $y=\tan\left(\frac{x}{3}\right)$.
Part 3: Vertical translation
Adding a nonzero number to a function results in translating its graph vertically: $$f(x) \longrightarrow f(x) + c$$ Let $g(x)=f(x)+c$.If $c<0$ the graph of $f(x)$ will be shifted down $c$ units to obtain $g(x)$.
If $c>0$ the graph of $f(x)$ will be shifted up $c$ units to obtain $g(x)$.
Example. Draw the graph of $y=x^2+5$.
Solution: We translate the graph of $y=x^2$ up by $5$ units to obtain the required graph.
The graph of $y=x^2+5$.
Part 4: Horizontal translation
Another transformation involves adding a nonzero number to the variable $x$: $$f(x) \longrightarrow f(x+d)$$ Let $g(x)=f(x+d)$.If $d<0$ the graph of $f(x)$ will be shifted $d$ units to the right to obtain $g(x)$.
If $d>0$ the graph of $f(x)$ will be shifted $d$ units to the left to obtain $g(x)$.
Example. Draw the graph of $y=e^{x-4}$.
Solution: Starting from the graph of $y=e^x$, we shift $4$ units to the right.
The graph of $y=e^{x-4}$.
We can also do a sequence of these transformations when more complicated graphs are involved.
Example. Draw the graph of $y=\frac{2}{\sqrt{4-x}}$.
Solution: Starting from the graph of $y=\frac{1}{\sqrt{x}}$, we perform vertical stretching, horizontal reflection and horizontal shift to get $y=\frac{2}{\sqrt{4-x}}$:
The graph of $y=\frac{2}{\sqrt{4-x}}$.
